题目描述
有一旅游胜地,可以看做是一个 n 个点、m 条边的连通无向图。每个点都有一个点权,编号为 i 的点的点权为 ai,表示这个点的景观值。
开发商为了能获取收益,准备选择一些点建设商业区,但是会让这些点的景观值大打折扣。具体地说,如果选择编号为 i 的点建设商业区,则会让该点的景观值变为 bi,其中 bi≤ai。
不过对于游客来讲,只要游览相邻的两个点时,景观值的差距不要太大就好。即确定好需要建设商业区的点后,记编号为 i 的点最终的点权为 wi,只要所有边 u,v 的 ∣wu−wv∣ 中最大值尽可能小即可。或者说,最小化有边相连的景观值差距的最大值。
请你帮助开发商计算所有可能的方案中,景观值最大差距的最小值。
开发商为了能获取收益,准备选择一些点建设商业区,但是会让这些点的景观值大打折扣。具体地说,如果选择编号为 i 的点建设商业区,则会让该点的景观值变为 bi,其中 bi≤ai。
不过对于游客来讲,只要游览相邻的两个点时,景观值的差距不要太大就好。即确定好需要建设商业区的点后,记编号为 i 的点最终的点权为 wi,只要所有边 u,v 的 ∣wu−wv∣ 中最大值尽可能小即可。或者说,最小化有边相连的景观值差距的最大值。
请你帮助开发商计算所有可能的方案中,景观值最大差距的最小值。
输入
第一行,两个正整数 n,m(2≤n≤105, n−1≤m≤min(n(n−1)/2,105) ),表示图的点数和边数。
第二行,共 n 个正整数 ai (1≤ai≤109),表示编号为 i 的点不建设商业区的景观值。
第三行,共 n 个正整数 bi (1≤bi≤109, bi≤ai),表示编号为 i 的点建设商业区后的景观值。
接下来 m 行,每行两个正整数 u,v,表示 u 和 v 有一条边相连。
数据保证图是连通的,也保证没有重边或自环。
第二行,共 n 个正整数 ai (1≤ai≤109),表示编号为 i 的点不建设商业区的景观值。
第三行,共 n 个正整数 bi (1≤bi≤109, bi≤ai),表示编号为 i 的点建设商业区后的景观值。
接下来 m 行,每行两个正整数 u,v,表示 u 和 v 有一条边相连。
数据保证图是连通的,也保证没有重边或自环。
输出
一个整数,景观值最大差距的最小值。
样例输入
Copy
4 3
10 7 5 5
6 2 1 2
2 4
3 2
2 1
样例输出 Copy
2
提示
样例输入二
6 6
8 8 7 6 9 9
7 4 6 3 4 7
3 1
4 3
5 1
2 4
1 6
4 1
样例输出二
2
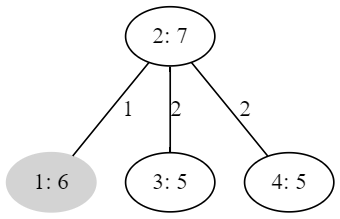
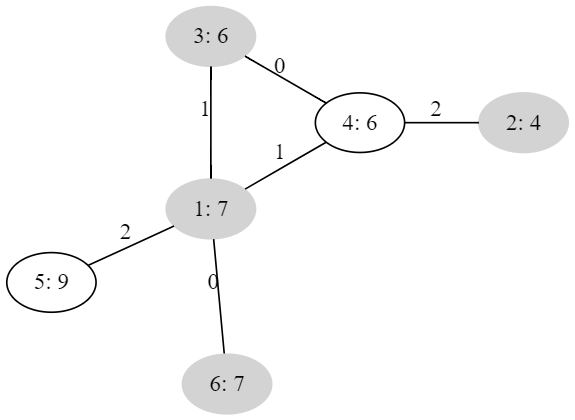
下面两图分别为两个样例的一个方案。点的标记为"编号:景观值",白色填充为没有建立商业区的点,灰色填充的为建立了商业区的点;边权为所连接的两个点的景观值差距。
第一个图中,只有点 1 建立了商业区,景观值最大差距为 2;第二个图中,点 1、2、3、6 建立了商业区,景观值最大差距为 2。
6 6
8 8 7 6 9 9
7 4 6 3 4 7
3 1
4 3
5 1
2 4
1 6
4 1
样例输出二
2
下面两图分别为两个样例的一个方案。点的标记为"编号:景观值",白色填充为没有建立商业区的点,灰色填充的为建立了商业区的点;边权为所连接的两个点的景观值差距。
第一个图中,只有点 1 建立了商业区,景观值最大差距为 2;第二个图中,点 1、2、3、6 建立了商业区,景观值最大差距为 2。

