题目描述
二叉树的递归定义如下:
1. 空树,即此树的根节点为一个叶子结点,空树用 Leaf 表示
2. 不是空树,即树存在一个根节点非叶子结点,其有一个标签 Label 可以存储这个节点的信息,并且这个根节点存在一个左分支和右分支,其左分支和右分支也是一颗二叉树,表示为 Node(Label, LeftTree, RightTree)
所以 :
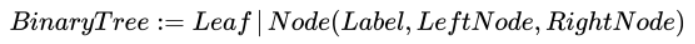
例如我们可以参照这样的形式用伪代码表示一颗二叉树, 其节点的 Label 存储一个整数
可以用伪代码表示如下
tree = Node( 1, Node (2, Node (5, Leaf, Leaf), Node (4, Leaf, Leaf)), Node (3, Node (6, Leaf, Leaf), Leaf) )
为了使处理方便,输入数据按照先节点值,后左子树数据,后右子树数据的前序方式输入,如
其中 0 表示叶子,也即为空树,这串数据与上方所给图片和伪代码表示同一棵树。
Jins 被指派去处理这样的树型数据,但是 Jins 觉得这还不够,恰巧 Jins 刚刚学习了二叉搜索树,他想让你帮助他处理这些数据。
二叉搜索树的定义如下:
对于一颗二叉搜索树而言,首先满足其是一棵二叉树,其次
1、对于一棵非空二叉搜索树,其根节点的值要严格大于其左子树中任意节点的值,严格小于其右子树中任意节点的值
2、其左子树和右子树也是一棵二叉搜索树
3、空树也是一颗二叉搜索树
但是 Jins 为了节省一些你的宝贵时间,他将二叉搜索树的定义修改了一下,并将具有这样性质的树命名为 Jins 树。
Jins 树定义如下:
对于一颗 Jins 树而言,首先满足其是一棵二叉树,其次
1、对于一棵非空 Jins 树,其根节点的值要严格大于其左子树中根节点的值,严格小于其右子树中根节点的值
2、其左子树和右子树也是一棵 Jins 树
3、空树也是一颗 Jins 树
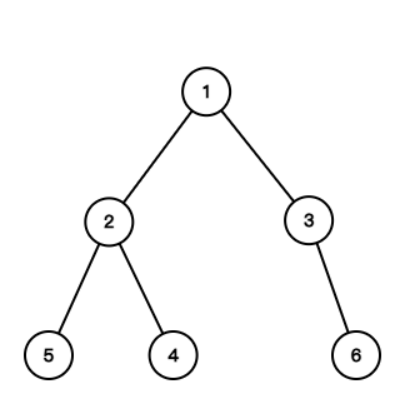
如图是一颗 Jins 树,而不是一颗二叉搜索树,因为节点值为 3 的右子树的根节点值为 10 (大于6)不满足二叉搜索树的第一条定义,而满足 Jins 树的定义。
Jins 会得到一些如上面介绍的树的前序遍历的数据,请聪明的你帮助他确定这些树是否是 Jins 树。
前序遍历:
1、先访问根结点;
2、再前序遍历左子树;
3、最后前序遍历右子树;
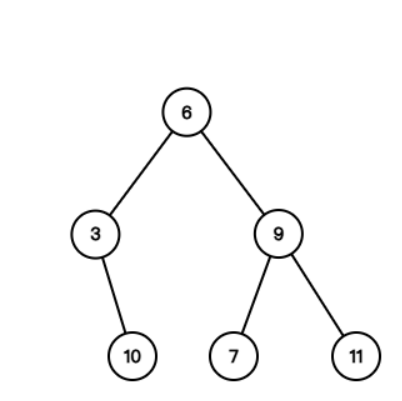
例如此二叉树前序遍历的结果为:1 -> 2 -> 5 -> 4 -> 3 -> 6
当然因为叶子节点的存在,所以遍历结果为:
1 -> 2 -> 5 -> 0 -> 0 -> 4 -> 0 -> 0 -> 3 -> 0 -> 6 -> 0 -> 0
1. 空树,即此树的根节点为一个叶子结点,空树用 Leaf 表示
2. 不是空树,即树存在一个根节点非叶子结点,其有一个标签 Label 可以存储这个节点的信息,并且这个根节点存在一个左分支和右分支,其左分支和右分支也是一颗二叉树,表示为 Node(Label, LeftTree, RightTree)
所以 :
例如我们可以参照这样的形式用伪代码表示一颗二叉树, 其节点的 Label 存储一个整数

可以用伪代码表示如下
tree = Node( 1, Node (2, Node (5, Leaf, Leaf), Node (4, Leaf, Leaf)), Node (3, Node (6, Leaf, Leaf), Leaf) )
为了使处理方便,输入数据按照先节点值,后左子树数据,后右子树数据的前序方式输入,如
1 2 5 0 0 4 0 0 3 6 0 0 0
其中 0 表示叶子,也即为空树,这串数据与上方所给图片和伪代码表示同一棵树。
Jins 被指派去处理这样的树型数据,但是 Jins 觉得这还不够,恰巧 Jins 刚刚学习了二叉搜索树,他想让你帮助他处理这些数据。
二叉搜索树的定义如下:
对于一颗二叉搜索树而言,首先满足其是一棵二叉树,其次
1、对于一棵非空二叉搜索树,其根节点的值要严格大于其左子树中任意节点的值,严格小于其右子树中任意节点的值
2、其左子树和右子树也是一棵二叉搜索树
3、空树也是一颗二叉搜索树
但是 Jins 为了节省一些你的宝贵时间,他将二叉搜索树的定义修改了一下,并将具有这样性质的树命名为 Jins 树。
Jins 树定义如下:
对于一颗 Jins 树而言,首先满足其是一棵二叉树,其次
1、对于一棵非空 Jins 树,其根节点的值要严格大于其左子树中根节点的值,严格小于其右子树中根节点的值
2、其左子树和右子树也是一棵 Jins 树
3、空树也是一颗 Jins 树

如图是一颗 Jins 树,而不是一颗二叉搜索树,因为节点值为 3 的右子树的根节点值为 10 (大于6)不满足二叉搜索树的第一条定义,而满足 Jins 树的定义。
Jins 会得到一些如上面介绍的树的前序遍历的数据,请聪明的你帮助他确定这些树是否是 Jins 树。
前序遍历:
1、先访问根结点;
2、再前序遍历左子树;
3、最后前序遍历右子树;

例如此二叉树前序遍历的结果为:1 -> 2 -> 5 -> 4 -> 3 -> 6
当然因为叶子节点的存在,所以遍历结果为:
1 -> 2 -> 5 -> 0 -> 0 -> 4 -> 0 -> 0 -> 3 -> 0 -> 6 -> 0 -> 0
输入
以前序遍历的方式输入一颗二叉树,树的节点数据为 int 型正整数, 以 0 表示空树
输出
若所给的二叉树是一颗Jins树,则输出 True ,否则输出 False
样例输入
Copy
1 2 5 0 0 4 0 0 3 6 0 0 0
样例输出 Copy
False
提示
样例输入 2
样例输出 2
10 1 0 0 12 0 0
样例输出 2
True