2312: Image Recognition
时间限制: 6 Sec 内存限制: 128 MB提交: 2 解决: 1
[状态] [讨论版] [提交] [命题人:]
The monitoring system without any person does not necessarily
require a large number of dynamic images. It is enough to transport an immobile image in ** seconds in most
practical condition.
In the JD-T warehouse, the goods is stored in
large cubical crates, all of which have the same dimensions. The crates are
stacked in neat piles, forming a three-dimensional grid. The remote online
monitoring system takes pictures of the piles once in S seconds using three cameras: a front camera, a side
camera and a top camera. The image from the front camera shows the height of
the tallest pile in each column, the image from the side camera shows the
height of the tallest pile in each row, and the image from the top camera shows
whether or not each pile is empty. If the monitoring system detects a change in any of the images,
it sounds an alarm.
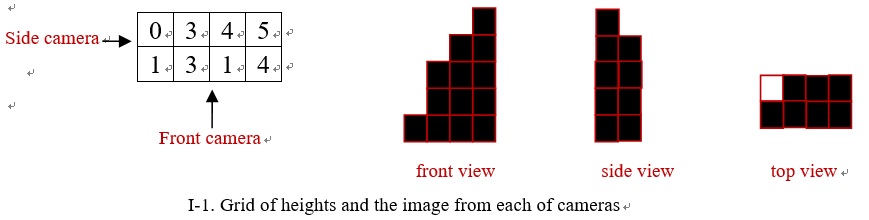
Figure I-1 shows a possible layout of the grid and the image
from each of the cameras.

Figure I-2 , I-3 and
figure I-1 have the same images from
each of the cameras.
A theft gang noticed
this unmanned warehouse. They found that it took T seconds to transport a
crate. They wants to steal as many crates as possible. Since they cannot
disable the monitoring system, they
plans to fool it by arranging the remaining crates into piles so that the next
set of camera images are the same.
Is the remote online monitoring system safe?
If it's not safe, the maximum number of crates that can be stolen while
leaving a configuration of crates that will fool the monitoring system, camera images remain unchanged.
The first line of the input
contains one integer T, which is the number of test cases (1<=T<=6). Each test case
specifies:
* Line 1: S T
(1<=S=1012 1<=T=103 )
* Line 2: m n
rows and columns in the grid, respectively. (1<=m, n<=100)
*Line 3..m+3: each
line contains n integers, the heights (in crates) of the piles in the corresponding row. ( all
heights are between 0 and 109 inclusive.)
For each test case , print the maximum number of crates that can
be stolen without being detected.
3
10000 100
5 5
1 4 0 5 2
2 1 2 0 1
0 2 3 4 4
0 3 0 3 1
1 2 2 1 1
10000 100
2 3
50 20 3
20 10 3
1000 99
2 3
50 20 3
20 10 3
9
30
10