2313: Jigsaw Puzzle
时间限制: 20 Sec 内存限制: 128 MB提交: 2 解决: 0
[状态] [讨论版] [提交] [命题人:]
Jigsaw puzzle is a
popular intellectual game for its . It is not only used for education and
entertainment, but also for commercial advertising and political propaganda. Maps, animal landscapes, characters,
etc. can be made into jigsaw puzzles.
A salesman named
Dimma began to sell jigsaw puzzles. It first partitioned a map into several rectangular tiles, then disrupt the
order. You need to rearrange it, spell
out the original map.
Suppose each fragment
is a rectangle of a*b , Dimma needs to cut
their printing costs by minimizing the number of rectangle used for their maps.
The left side of Figure J-1 shows 8 rectangles to cover a map. The right side shows how you can
cover the same map with only 6 rectangles.
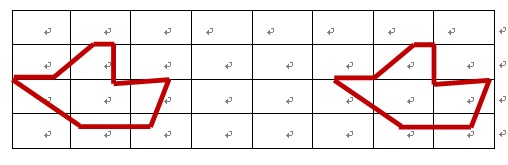
Your task is to help Dimma find the minimum number of rectangles needed to cover a given map. For simplicity, the map will be given as a closed polygon that does not intersect itself.
* Line 1: n a b (3 ≤ n ≤ 50 1 ≤ a, b ≤ 100)
n is the number of polygon vertices , a
and b are the
dimensions of each rectangle.
*Line 2~ n+1: xi yi ( 0≤ xi≤ 10*a 0≤ yi≤ 10*b i=1…. n )
Each of the next n lines contains two integers xi nad yi
specifying the vertices of the polygon representing the region (in either
clockwise or counter-clockwise order).
print the minimal
number of tiles necessary to cover the whole interior of the polygon.
12 9 9
1 8
1 16
6 16
9 29
19 31
23 24
30 23
29 18
20 12
22 8
14 0
14 8
10