题目描述
X星球附件的其他星球的矿产资源几乎都被采集完了,现在去采集资源就要去更远的地方。
所以采矿的成本急剧增加。矿工们希望到达一个星球能带走尽量多的矿产。但是飞船的容量是有限的,
而且飞船上没有能分割矿产的工具。所以对于一块矿产只能选择带走或者不带走。起初矿工把所有的
矿产按重量排序优先带走最重的。可是发现这样并不是最优的,例如飞船容量S=6,矿产为:4 3 3时
带走3 3才是最优的。 后来他们希望通过计算机解决。
他们的想法是通过计算机枚举每一种可能的方案来求得最大值。
例如带走1块有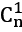 种方案。带走2块有
种方案。带走2块有 种方案.......带走n块有
种方案.......带走n块有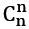 种方案
种方案
所以一共有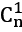 +
+ +......+
+......+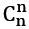 =(2^n)-1种方案。只要计算机把每一种方案得到矿产都计算出来,
=(2^n)-1种方案。只要计算机把每一种方案得到矿产都计算出来,
再取最大值就行了。后来才发现这样是不可行的。假如n=1000,那么(2^1000)=10^301。 X星球的
普通计算机和地球运算最快的计算机一样快(2018年:Summit: 3^18次/秒)。那么也要3.3*10^283秒。
一年有3.2*10^7秒也就是需要10^276年。显然是不可行的。
你的导师是X星球最有名的算法科学家。他们就向你的导师请教这个问题,你的导师很快就设计
一个算法能够在O(n*s)的时间得到最优解(0-1背包)。也就是说n=10^9, s=10^9时(10^18次/s)的计算
机正好能用1秒计算出最优解。
当然你也参与了其中。你的导师让你计算对于一个容量为S*10^9,矿产数量为n*10^9和一个计算
速度为(v*10^18次/s)的计算机。用这个优化后的算法能在几秒内计算出最优解。
所以采矿的成本急剧增加。矿工们希望到达一个星球能带走尽量多的矿产。但是飞船的容量是有限的,
而且飞船上没有能分割矿产的工具。所以对于一块矿产只能选择带走或者不带走。起初矿工把所有的
矿产按重量排序优先带走最重的。可是发现这样并不是最优的,例如飞船容量S=6,矿产为:4 3 3时
带走3 3才是最优的。 后来他们希望通过计算机解决。
他们的想法是通过计算机枚举每一种可能的方案来求得最大值。
例如带走1块有
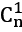 种方案。带走2块有
种方案。带走2块有 种方案.......带走n块有
种方案.......带走n块有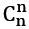 种方案
种方案 所以一共有
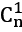 +
+ +......+
+......+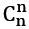 =(2^n)-1种方案。只要计算机把每一种方案得到矿产都计算出来,
=(2^n)-1种方案。只要计算机把每一种方案得到矿产都计算出来, 再取最大值就行了。后来才发现这样是不可行的。假如n=1000,那么(2^1000)=10^301。 X星球的
普通计算机和地球运算最快的计算机一样快(2018年:Summit: 3^18次/秒)。那么也要3.3*10^283秒。
一年有3.2*10^7秒也就是需要10^276年。显然是不可行的。
你的导师是X星球最有名的算法科学家。他们就向你的导师请教这个问题,你的导师很快就设计
一个算法能够在O(n*s)的时间得到最优解(0-1背包)。也就是说n=10^9, s=10^9时(10^18次/s)的计算
机正好能用1秒计算出最优解。
当然你也参与了其中。你的导师让你计算对于一个容量为S*10^9,矿产数量为n*10^9和一个计算
速度为(v*10^18次/s)的计算机。用这个优化后的算法能在几秒内计算出最优解。
输入
多样例测试
第一行输入样例数:T
对于每个样例:输入S n v (0<s,n<10^7, 0<v<10^7)
第一行输入样例数:T
对于每个样例:输入S n v (0<s,n<10^7, 0<v<10^7)
输出
对于每个样例输出:计算机能在几秒内计算出最优解(对于小数部分向上取整)。
样例输入
Copy
2
3 3 9
3 2 5
样例输出 Copy
1
2