2828: 五个小时卷积神经网络从入门到入土
时间限制: 1 Sec 内存限制: 128 MB提交: 17 解决: 9
[状态] [讨论版] [提交] [命题人:]
 tle="" align="" />
tle="" align="" />
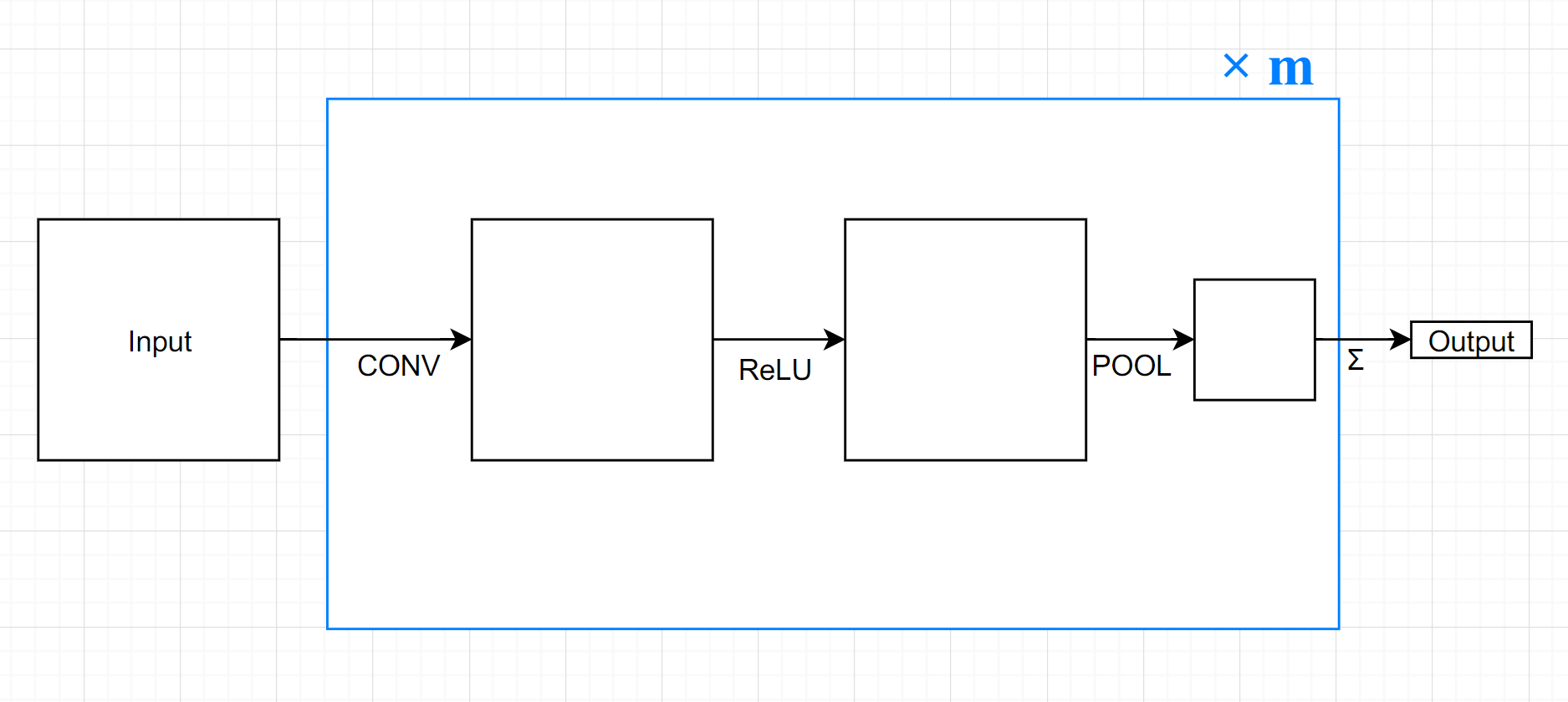
输入层是 n∗n 的黑白图像,输出层的值是上一层的各个元素的和
隐含层包括: 卷积前使用 pad=2 的 Zero-padding, 卷积核大小为 3∗3(f=3),stride=1 对于所有层权值共享, 激活函数为 ReLU , 池化前使用 pad=1 的 Zero-padding 池化使用的是 2∗2 Average pooling (默认 stride=2),网络深度为 m 层 (即重复执行前面几种操作m次)
尽管卷王神经网络的准确率已经超过 100%, 卷王小辣对它的效率还是不够满意,你能帮他快速卷出神经网络的输出值吗
输出答案 %998244353 的值。假设答案是P/Q,那么你应该输出 P×Q−1,这里 Q−1 表示 Q 在模 998244353 意义下的逆元。
以下是一些关于卷积神经网络的小知识
卷积神经网络(Convolutional Neural Networks, CNN)是一类包含卷积计算且具有深度结构的前馈神经网络,是深度学习的代表算法之一。
基础的CNN由 卷积(convolution), 激活(activation), 池化(pooling)三种结构组成。
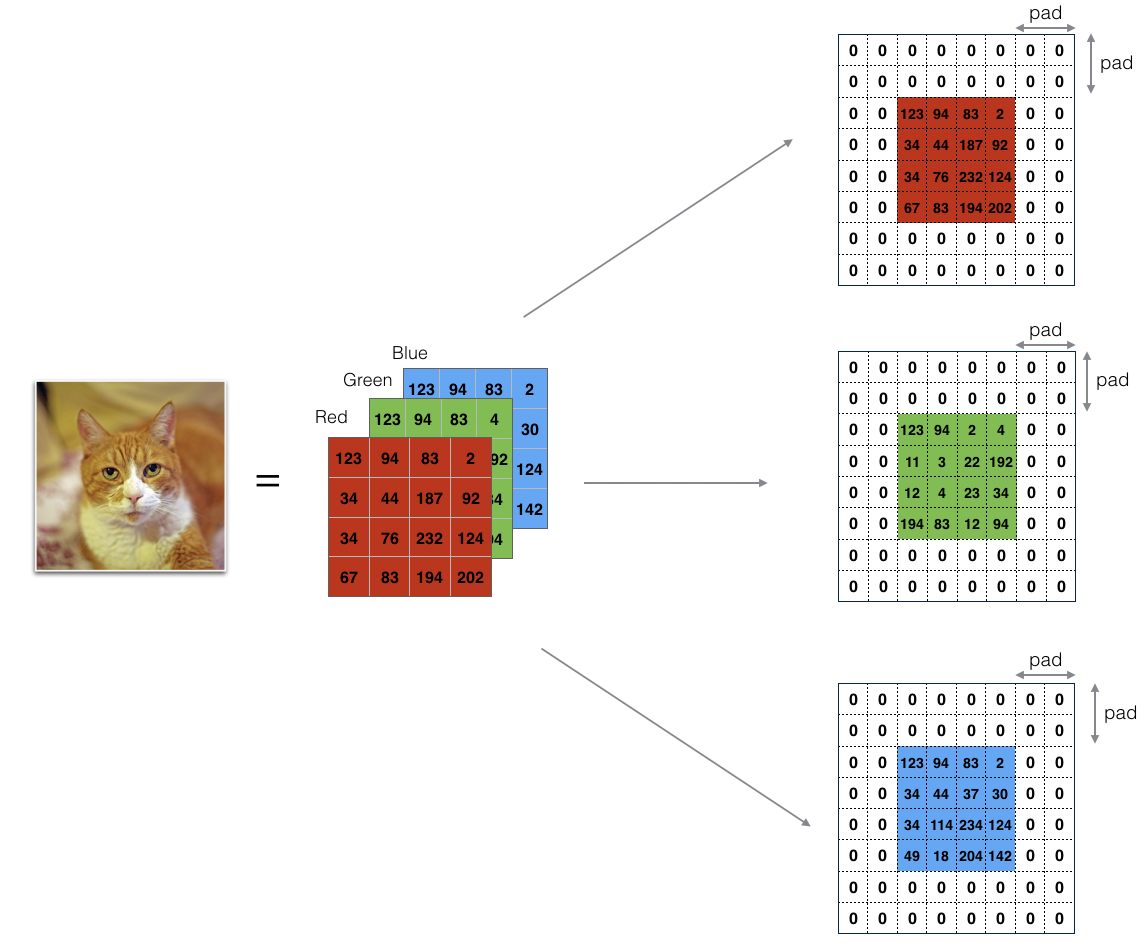
零填充(Zero-padding) 是在图像周围填充 0。 图示为 pad=2 的情况
 tle="" align="" />
tle="" align="" />
卷积部分是核心操作,通俗的说:
定义卷积核大小为 f×f, 权值为 wi,j
步长为 stride

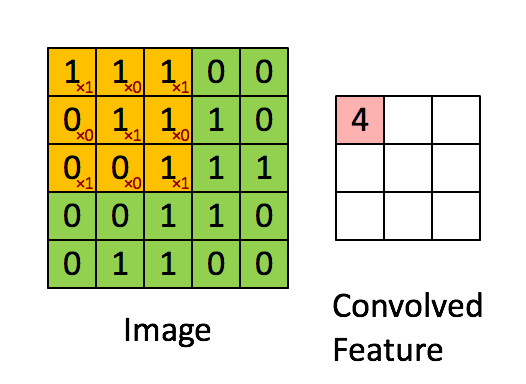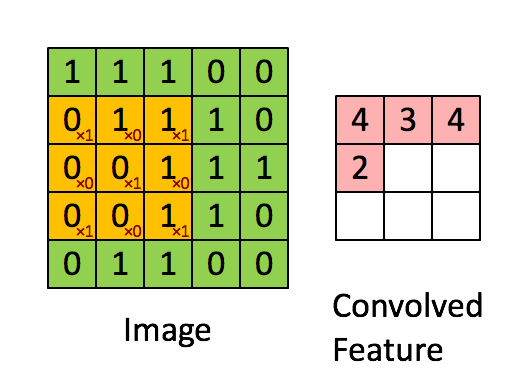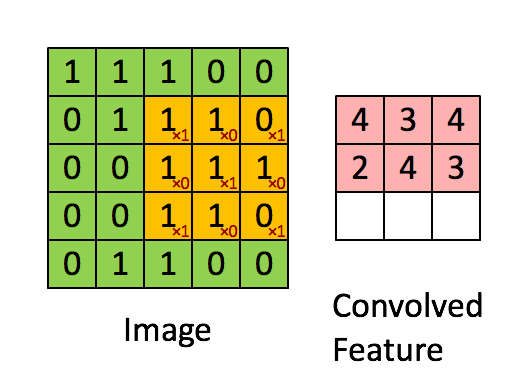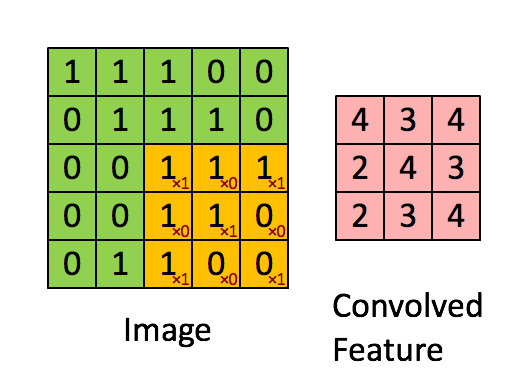
卷积之后,通常引入非线性激活函数(activation function),这里定义 activation function 是 h()
经过激活函数后,得到的结果是 Zx,y=h(Ax,y)
其中,线性整流单元(ReLU)为函数 h(x)=max(0,x)
池化(pooling),是一种降采样操作(subsampling),主要目标是降低feature maps的特征空间,或者可以认为是降低feature maps的分辨率。
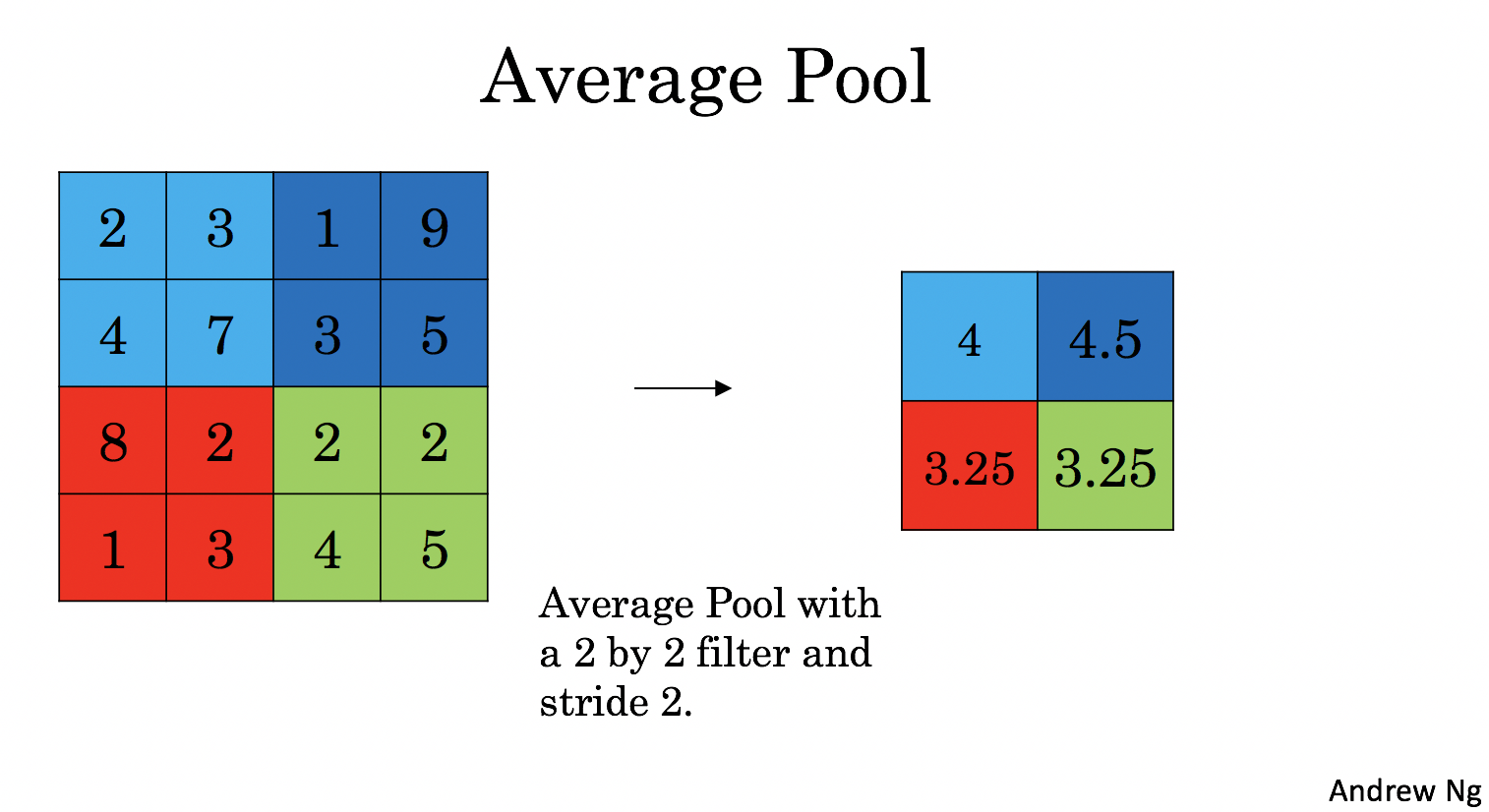
平均值池化 Average pooling: 如下图所示, 2∗2 的average pooling就是取 4 个像素点中平均值值保留,默认 stride=2
平均池化可等价看成 f=2,stride=2 卷积核为 的卷积(如果 nprev 为奇数计算时向下取整,详情见卷积公式)
的卷积(如果 nprev 为奇数计算时向下取整,详情见卷积公式)
 tle="" align="" />
tle="" align="" />
现在你已经是个成熟的卷怪了,快和小辣一起卷吧!
第一行一个整数 T, 表示数据组数。对于每组数据:
第一行 2 个整数 n,m 表示输入的图像尺寸和神经网络深度
接下来三行每行三个整数,表示卷积核的权值w
接下来 n 行每行长度为 n 的01串, 表示每个像素点的值0表示黑1表示白
T≤20,1≤n≤103,0≤m≤2×105,0≤wi,j≤109
3
1 0
0 0 0
0 0 0
0 0 0
0
1 1
1 0 1
1 0 1
1 0 1
1
30 10
1 1 1
0 0 0
1 1 1
000000000000000000000000000000
000000000000000000000000000000
000000000000000000000000000000
000000000000010000000000000000
000000111000111000001100000000
000000111100111000011100000000
000000001110111000111000000000
000000000111110001111000000000
000111111111111111111111000000
000111111111111111111111000000
000000000000110000000000000000
000000000001110000000000000000
000000000001100000000000000000
001111111111111111111111110000
001111111111111111111111100000
000000001111000000111000000000
000000011111111111011100000000
000001111111111111111111000000
000111111100000001110111110000
001111101100000000110011111000
001110001100000000110000111000
000000001100011001110000000000
000000001100111111100011000000
000000001100001111000111000000
000000001100000000000110000000
000000001100000000001110000000
000000001111111111111110000000
000000000111111111111100000000
000000000000000000000000000000
000000000000000000000000000000
0
499122178
448445996
部分图片来源 deeplearning.ai
部分描述来源于网络
样例2解释
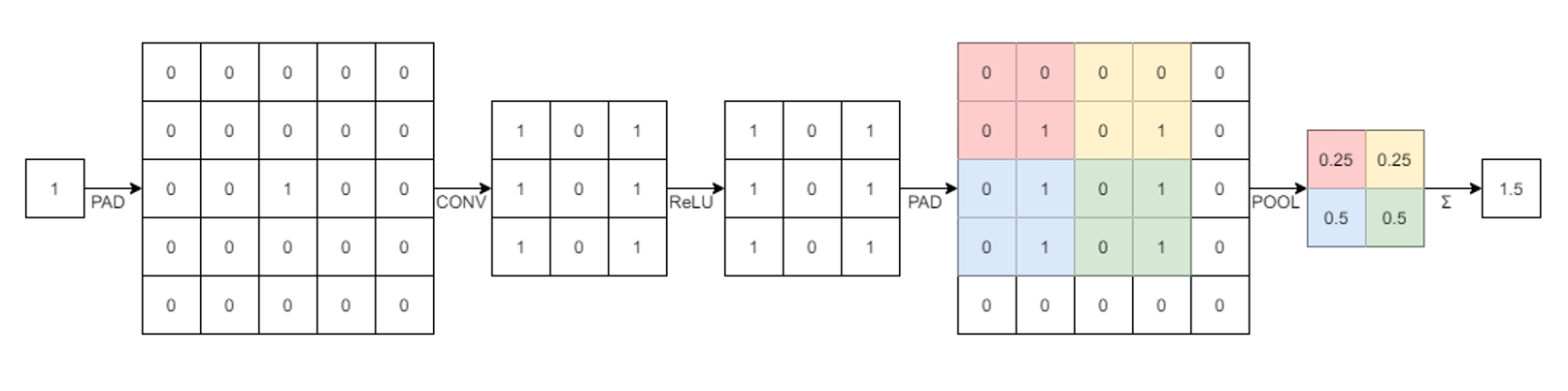 tle="" align="" />
tle="" align="" />