2982: 章节三:我本想成为一个剑士,可命运却将我推向奶妈
时间限制: 1 Sec 内存限制: 128 MB提交: 197 解决: 46
[状态] [讨论版] [提交] [命题人:]
题目描述
黄瑞士三人跟随达达尼昂阁下运送魔物的尸体到达了营地,达达尼昂热情的留下三人随伙吃饭。
黄瑞士提出想要加入达达尼昂一行人的讨伐队伍一同去讨伐黑龙王。
"是吗?真是有理想的年轻人啊,给我看看你们的本领怎么样吧!"
黄瑞士抽出宝剑,在达达尼昂阁下面前殷勤演练起了他自创的赶苍蝇剑法。
达达尼昂微不可查的抖了抖眉头。
"不错的本领,有兴趣加入我们的炊事班吗?"
温锦鹏见状赶忙说:"他还是一个会治愈魔法的魔法师!"
"哦?是吗?"达达尼昂提起了兴趣。
黄瑞士抖开魔法卷轴,端详起了上面所画的三个魔法阵。
————————————————————————————
每个魔法阵都是一个由若干连接和节点构成的网络
法术卷轴给出了每个魔法阵的参数和使用提示,还给出了使用它们的咒语,只是咒语的关键部分有些模糊不清
请仔细参考卷轴的提示,帮助黄瑞士向达达尼昂演示治愈魔法。
黄瑞士提出想要加入达达尼昂一行人的讨伐队伍一同去讨伐黑龙王。
"是吗?真是有理想的年轻人啊,给我看看你们的本领怎么样吧!"
黄瑞士抽出宝剑,在达达尼昂阁下面前殷勤演练起了他自创的赶苍蝇剑法。
达达尼昂微不可查的抖了抖眉头。
"不错的本领,有兴趣加入我们的炊事班吗?"
温锦鹏见状赶忙说:"他还是一个会治愈魔法的魔法师!"
"哦?是吗?"达达尼昂提起了兴趣。
黄瑞士抖开魔法卷轴,端详起了上面所画的三个魔法阵。
————————————————————————————
每个魔法阵都是一个由若干连接和节点构成的网络
法术卷轴给出了每个魔法阵的参数和使用提示,还给出了使用它们的咒语,只是咒语的关键部分有些模糊不清
请仔细参考卷轴的提示,帮助黄瑞士向达达尼昂演示治愈魔法。
输入
输入将依次给出三个魔法网络
每个魔法网络输入第一行给出n,m,k三个整数[1,20],分别表示每层网络的结点个数,网络中间节点层(见样例提示hidden layers)的层数 ,以及输入魔力波动向量的长度
第二行给出一个字符串s 属于{“ReLU”,“Sigmoid”,“None”} 代表激活函数的类别(激活函数的含义见样例提示,None表示不需要激活函数)
接下来一行给出k个实数,表示输入魔法阵的魔力波动向量(含义见样例提示)
接下来一行给出n*k个实数,表示输入向量连接到第一层hidden layer的参数向量(含义见样例提示)
接下来m-1行,每行n*n个实数,每行表示每两行hidden layer之间的参数向量(含义见样例提示)
接下来一行给出n个实数,表示hidden layer到输出节点的参数向量(含义见样例提示)
接下来m行每行给出n个实数,表示每层网络节点的偏置(偏置含义见样例提示)
然后一行给出一个实数表示最后的输出节点的偏置(偏置含义见样例提示)
自然常数e取值 e=2.718
每个魔法网络输入第一行给出n,m,k三个整数[1,20],分别表示每层网络的结点个数,网络中间节点层(见样例提示hidden la
第二行给出一个字符串s 属于{“ReLU”,“Sigmoid”,“None”} 代表激活函数的类别(激活函数的含义见样例提示,None表示不需要激活函数)
接下来一行给出k个实数,表示输入魔法阵的魔力波动向量(含义见样例提示)
接下来一行给出n*k个实数,表示输入向量连接到第一层hidden la
接下来m-1行,每行n*n个实数,每行表示每两行hidden la
接下来一行给出n个实数,表示hidden la
接下来m行每行给出n个实数,表示每层网络节点的偏置(偏置含义见样例提示)
然后一行给出一个实数表示最后的输出节点的偏置(偏置含义见样例提示)
自然常数e取值 e=2.718
输出
按从大到小的顺序输出网络的输出值,输出保留两位小数
样例输入
Copy
2 2 3
None
1 1 1
1 2 3 4 5 6
1 1 2 2
2 1
0 0
0 0
0
2 2 3
ReLU
1 1 1
1 2 3 -4 5 -6
-1 1 2 2
2 1
0 1
2 3
4
2 2 3
ReLU
1 1 1
1 2 3 -4 5 -6
-1 1 2 2
2 -1
0 0
0 0
0
样例输出 Copy
84.00 19.00 0.00
提示
激活函数:ReLU(x) = max(0,x), Sigmoid(x) = 1 / (1 + exp(-x))
None表示无激活函数,也可以理解为 None(x) = x


输入样例中的第二个网络结构如下图所示:
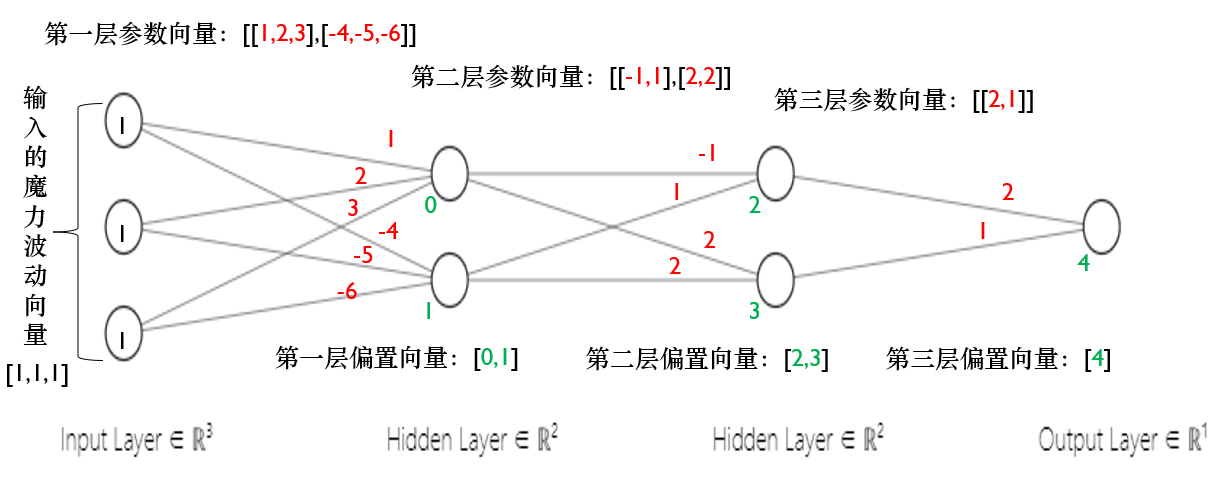
计算过程介绍:

魔法卷轴上的部分魔咒:
/*
C++中的容器:vector 向量,或者说动态数组的使用方法:
定义一个元素类型为double的动态数组:
vector<double> vec;
向动态数组中加入1到n共n个整数:
for(int i=1;i<=n;i++)
vec.push_back(i);
获得动态数组的长度:
int len = vec.size();
遍历并输出动态数组:
for(int i=0;i<len;i++)
cout<<vec[i]<<' ';
*/
#include<bits/stdc++.h>
using namespace std;
void read_vector(vector<double> &vec, int len) //读入一个向量
{
double x;
for(int i=1;i<=len;i++) {
cin>>x;
vec.push_back(x);
}
}
void read(vector<vector<double> > &in_paras, int len_in, int len_out) //读入一层参数,入口长度为len_in,出口为len_out
{
for(int i=1;i<=len_out;i++) {
vector<double> in_para;
read_vector(in_para, len_in);
in_paras.push_back(in_para);
}
}
string type;
const double e = 2.718;
double activate(double x) //激活函数
{
if(type=="Sigmoid") {
//这一部分变得模糊不清
}
double dot(vector<double> &in, vector<double> &in_para) //向量的点积
{
int len1 = in.size();
//这一部分变得模糊不清
}
vector<double> get(vector<double> &in, vector<vector<double> > &in_paras, vector<double> &bias) //对于输入向量,经过与参数层in_paras的运算,得到输出向量
{
vector<double> outs;
int len_out = in_paras.size();
for(int i=0;i<len_out;i++) {
double out = activate(dot(in, in_paras[i])+bias[i]);
outs.push_back(out);
}
return outs;
}
double solve()
{
int n, m, k;
cin>>n>>m>>k;
cin>>type;
vector<double> in;
read_vector(in, k);
vector<vector<double> > in_paras[m+5];
read(in_paras[1], k, n);
for(int i=2;i<=m;i++)
read(in_paras[i], n, n);
read(in_paras[m+1], n, 1);
vector<double> bias[m+5];
for(int i=1;i<=m;i++) read_vector(bias[i], n);
read_vector(bias[m+1], 1);
for(int i=1;i<=m+1;i++) {
in = get(in, in_paras[i], bias[i]);
}
return in[0];
}
// 这题真的很简单啊,运气只奖励给勇者!
int main () {
vector<int> ans;
double x = solve();
double y = solve();
double z = solve();
if(y>x) swap(x, y);
if(z>y) swap(z, y);
if(y>x) swap(x, y);
printf("%.2f %.2f %.2f\n", x, y, z);
}