《Noita》是一个轻度 Rogue-like 的魔法动作游戏，同时也是一款魔法编程游戏，玩家可以通过拿到的法术按照释放顺序放入法杖中，从而制造一把威力无比的法杖去击败强大的敌人。

法杖中的法术会按照从左往右的顺序依次释放，当法杖中所有的法术都施放结束后（每个法术都会有它自己的施放时间），会进入充能时间，充能时间结束后将进入下一个周期（循环这个过程）

现在你的手上拥有一把充能时间为 0.05s 法术容量无穷大（可以容纳无数个法术）的法杖，以及 n 个伤害为 3，施放延迟为 0.05s 的火花弹（施放延迟指施放这个法术一次所需要的时间）。
现在你进入神圣之山购买了 m 个奇怪的修正法术（这修正法术只对火花弹有影响，并且对火花弹的影响可以重叠，但是修正法术之间不会互相影响），修正法术没有释放延迟。

• 修正法术会使得在修正法术之后的所有火花弹的 伤害增加 10 但是 每个火花弹的 施放延迟增加 0.05s（施放延迟变为 0.10s）
  

请问如何组装法杖可以使得平均每秒伤害达到最大值（不考虑暴击以及题目描述外的额外伤害）（输出答案和标准答案误差小于 0.01 即表示答案正确）

• 平均每秒伤害计算公式：ADPS = 一个周期内所有法术修正后的伤害之和 ÷ (一个周期内所有法术的释放延迟所需时间之和 + 法杖充能时间)

---

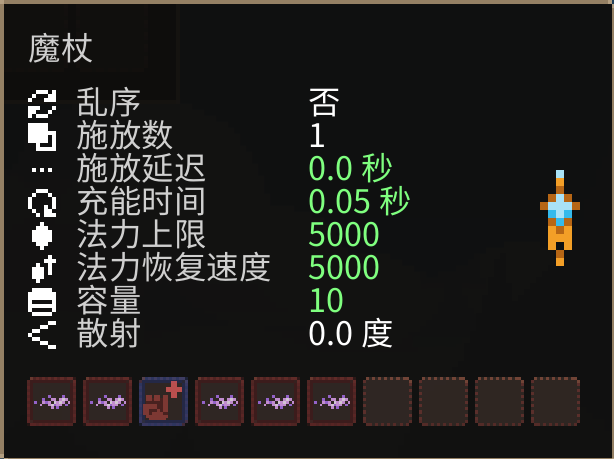
如图所示的法杖有 5 个火花弹和 1 个修正法术，这个修正法术的后面有 3 个火花弹它们的伤害值为 13 施放延迟 0.10s，前 2 个火花弹的伤害为 3 施放延迟为 0.05s。

• 一个周期内所有法术修正后的伤害之和 = 3*2 + 13*3 
• 一个周期内所有法术的释放延迟所需时间之和 = 0.05*2 + 0.10*3
• 法杖充能时间 = 0.05

注意：这种做法得到的不一定是最大值

本题有多个实例
第一行输入一个正整数 T 表示一共有 T 组数据
接下来 T 行每组一行两个正整数 n，m 分别表示你手上有 n 个火花弹，以及购买了 m 个奇怪的修正法术

数据范围

• 1 <= T <= 10000
• 1 <= n <= 1000
• 1 <= m <= 1000

一共 T 行，每行一个浮点型表示答案（输出答案和标准答案误差小于 0.01 即表示答案正确）

• 充能时间：当法杖释放完法杖中的所以法术后有一个充能时间，在这个充能时间中，任何法术都无法施放，充能时间结束后代表这个周期结束，进入下一个周期
• 施放延迟：施放这个法术所需要的时间

 23级新生C语言周赛